|
BULANIK MANTIK NEDİR ?
Zor ve karışık Aristo mantığı yerine son 30-40 yıldır geliştirilen bulanık
mantık ile çok karmaşık sorunlar çok basit şekilde çözülebiliyor.
Bulanık Mantık (BM) aristo(Batı) mantığının eksiklik, zorluk veya yanlışlıklarını
giderebilmek için Azeri bilim adamı Prof. Lütfi A.Zade tarafından geliştirilmiştir.aristo mantığında
bilindiği gibi bir şey ya A kümesinin elemanıdır yada değildir. yani ya siyah yada beyaz.(ya bizimlesiniz
yada düşmanla sözünün altındaki mantık gibi.) gerçekte tam siyah veya tam beyazı bulamazsınız.
Aristo mantığı bunları yok sayar. BM ise gerçek hayata uygun olarak hemen hemen tamamıyla grilerle
çalışır. çok uç durumlarda siyah veya beyaz vardır. (Doğunun güzel düşünce iklimi). Batı
hala BM yi anlayamıyor. BM japonyada çinde ve Türkiye'de aselsanda ve evrenkentlerde geliştirilmektedir.
BM'ı anlamanın en iyi yolu bir örneği incelemektir. Bunun için makine mühendisliğinde malzeme seçimi için
örnek yazılım geliştirelim. malzeme seçimine etki eden iki etkeni alalım.(etken sayısını
çok fazlalaştırabiliriz, ancak örneğin anlaşılmasının kolaylaşması için iki etkeni
alıyoruz.)etkenlerden birisi malzemenin sertliği diğeri ise malzemenin işlenebilirliği olsun. sonuç
ise malzeme kalitesi olarak çıksın. BM insani değerlendirmeleri kullanabildiğimiz bir mantıktır.
(Sıcak soğuk hızlı yavaş sert yumuşak gibi)
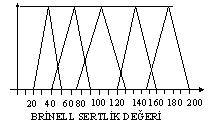
Malzeme sertliğini 5 gruba ayıralım.Bunlar Çok az Sert (ÇOS), Az Sert(AS), Sert(S), Oldukça Sert(OS), Çok sert
(ÇS) olsun. sertlik birimi olarak brinell i seçelim.
20-50 brinell arası ÇOS,40-80 arası AS,65-120 arası S 110-160 arası OS 145-200 arası da ÇS olsun.
yan resimde bu değerlere göre grafiği gösterilmektedir.
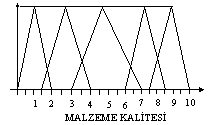
Malzemenin işlenebilirliğinide 5 gruba ayıralım. bunlar 1-Çok kötü işlenir(ÇKİ)2- Kötü işlenir
(Kİ) 3-Orta İşlenir(Oİ) 4- İyi İşlenir(İİ) ve 5- Çok iyi işlenir(Çİİ)
olsun.İşlenebilirliği 0-10 arası değerlendirelim. 0-2 ÇKİ, 1.5-4 Kİ, 3-7 Oİ, 6-8,5
İİ ve 7.5-10 Çİİ olsun. işlenebilirlik grafiğide yanda gösterilmiştir.

Şimdi bu iki özelliğe bağlı olarak malzeme kalitemizin ne olacağını değerlendirelim.mlz
kalitesinide 5 gruba ayıralım. bunlar 1- Çok kötü kalite (ÇKK) 2- Kötü kalite (KK) 3-Orta kalite(OK) 4-İyi
kalite(İK) ve 5- Çok iyi kalite(ÇİK) olsun.değerleri işlenebilirlikte olduğu gibi 1-10 arası
grup değerleride aynı olsun.bunun grafiği de yandadır
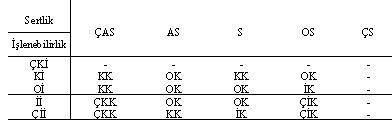
KURAL TABANI
Kural tabanı oluşturabilmek için incelenen konuyu iyi bilmek gerekir. yan tarafta kural tabanı tablosunu oluşturdum.
bu örneğimiz için değişik sonuçlar verecek şekilde tanımlanmıştır.kural tabanını
oluşturduktan sonra eğer ise tanımlamarı yapılabilir.
Eğer işlenebilirlik çok iyi ise ve sertlik az sert ise orta kalite ürün alırız.
Eğer işlenebilirlik çok iyi ise ve sertlik oldukça sert ise çok iyi kalite ürün alırız.
Eğer işlenebilirlik iyi ise ve sertlik çok az sert ise çok kötü kalite ürün alırız.
Eğer işlenebilirlik iyi ise ve sertlik normal sert ise oldukça kalite ürün alırız.
bunları kural tabanı grafiğinde gösterildiği şekilde her durum için ayrı ayrı yazabiliriz.
ÇIKARIM
Bulanık küme elemanı haline getirdiğimiz giriş öğelerini şimdi durulaştırarak geçirerek
kullanılabilir sonuçlara dönüştürmeliyiz. buna çıkarım denir. Örneğimizdeki malzeme sertliği
70 brinell işlenebilirliği içinde 6.5 olsun.
70 brinel için ortalama alırsak.Az sert bölge için x1=(80-40)/(80-70)=5. Sert bölge için x2=(120-65)/(120-75)=1.22 bulunur.5
için 5 ve 1.22 toplamı yüzde olarak, c1=5*100/6.22= %80=0.8. 1.22 içinde c2=1.22*100/6.22=%20=0.2 bulunur. Bunun anlamı
az sert= 0.8 sert=0.2 katsayılarıdır.
Yukarıdaki uygulamayı işenebilirlik için yaparsak.6.5 seviyesi orta ve iyi işlenebilme seviyelerindedir.
x1=(70-30)/(70-65)=8 x2=(80-60)/(80-65)=1.33 c1=8*100/9.33=%85=0.85 c2=%15=0.15 bulunur. orta işlenme 0.85 iyi işlenme
0.15 tir.
bu sonuçlara göre
1-az sert 0.8 VE orta işlenme 0.85
2-az sert 0.8 VE iyi işlenme 0.15
3-sert 0.2 VE orta işlenme 0.85
4-sert 0.2 VE iyi işlenme 0.15
olur. Bulanık mantıkta ve işlemi en düşük değeri alınır. veya işleminde en yüksek
değer alınır.
0.8 VE 0.85 - 0.8 Çok iyi kalite
0.8 ve 0.15 - 0.15 Çok kötü kalite
0.2 ve 0.85 - 0.2 Kötü kalite
0.2 ve 0.15 - 0.15 Çok kötü kalite
demektir.
bundan sonra değişik yöntemler uygulanır. basit 2 yöntemle çalışacağız.
VEYA YÖNTEMİ
0.8 VEYA 0.15 VEYA 0.2 VEYA 0.15 - 0.8
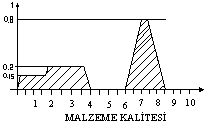
mlzeme kalitesini 0-10 arası derecelendirdiğimizden 0.8*(10-0)=8 değeri bulunur. Kalite grafiğimizde 8
nci kalite grubuna girer. İyi kalite bir malzememiz var demektir.
ALAN YÖNTEMİ.
0.8 VE 0.85 - 0.8 Çok iyi kalite
0.8 ve 0.15 - 0.15 Çok kötü kalite
0.2 ve 0.85 - 0.2 Kötü kalite
0.2 ve 0.15 - 0.15 Çok kötü kalite
bulduğumuz tüm değerleri kalite grafiğinde yerine koyarız ve daha üst değerleri keseriz. ortaya çıkan
alanın ağırlık merkezi bize malzeme kalitesini verir. Grafikte gösterilen alanları tek tek hesaplayıp
dik eksene göre uzaklıklarına göre ağırlık merkezi
g=1.alan*1.uzaklık+2.alan*2.uzaklık+3.alan*3.uzaklık)/(alanların toplamı) ifadesiyle sonuç bulunur.
alan ağırlık merkezi yöntemine göre buradaki sonuç 6.2 çıkmaktadır. Yine iyi kalite bi malzeme kullanıyoruz
demektir.
DEĞERLENDİRME
BM ile birbiriyle sadece mantık olarak ilişki kurabildiğimiz fakat matematiksel bir bağıntıya
dönüştüremediğimiz çoğu olayı çözebiliriz. bununla ilgili geliştirilen bilgisayar yazılımları
çık iyi sonuçlar vermektedir. Burada en önemli sorun kural tabanını çok iyi kurmalıyız. bu da insanlığın
bu güne kadarki deneyimlerini en açık şekilde kullanarak mümkündür.
|



